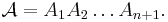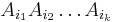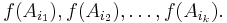Sperner's lemma

You may be looking for Sperner's theorem on set families

In mathematics, Sperner's lemma is a combinatorial analog of the Brouwer fixed point theorem, which follows from it. Sperner's lemma states that every Sperner coloring (described below) of a triangulation of an n-dimensional simplex contains a cell colored with a complete set of colors. The initial result of this kind was proved by Emanuel Sperner, in relation with proofs of invariance of domain. Sperner colorings have been used for effective computation of fixed points, in root-finding algorithms, and are applied in fair division (cake cutting) algorithms.

According to the Soviet Mathematical Encyclopaedia (ed. I.M. Vinogradov), a related 1929 theorem (of Knaster, Borsuk and Mazurkiewicz) has also become known as the Sperner lemma - this point is discussed in the English translation (ed. M. Hazewinkel). It is now commonly known as the Knaster–Kuratowski–Mazurkiewicz lemma.

Contents

One-dimensional case

In one dimension, Sperner's Lemma can be regarded as a discrete version of the Intermediate Value Theorem. In this case, it essentially says that if a discrete function takes only the values 0 and 1, begins at the value 0 and ends at the value 1, then it must switch values an odd number of times.

Two-dimensional case

The two-dimensional case is the one referred to most frequently. It is stated as follows:

Given a triangle ABC, and a triangulation T of the triangle. The set S of vertices of T is colored with three colors in such a way that

  1. A, B and C are colored 1, 2 and 3 respectively
  2. Each vertex on an edge of ABC is to be colored only with one of the two colors of the ends of its edge. For example, each vertex on AC must have a color either 1 or 3.

Then there exists a triangle from T, whose vertices are colored with the three different colors. More generally, there must be an odd number of such triangles.

Multidimensional case

In the general case the lemma refers to a n-dimensional simplex

\mathcal{A}=A_1 A_2 \ldots A_{n%2B1}.

We consider a triangulation T which is a disjoint division of 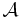\mathcal{A} into smaller n-dimensional simplices. Denote the coloring function as f : S → {1,2,3,...,n,n+1}, where S is again the set of vertices of T. The rules of coloring are:

  1. The vertices of the large simplex are colored with different colors, i. e. f(Ai) = i for 1 ≤ i ≤ n+1.
  2. Vertices of T located on any given k-dimensional subface
A_{i_1}A_{i_2}\ldots A_{i_k}
are colored only with the colors
f(A_{i_1}),f(A_{i_2}),\ldots,f(A_{i_k}).

Then there exists an odd number of simplices from T, whose vertices are colored with all n+1 colors. In particular, there must be at least one.

Proof

We shall first address the two-dimensional case. Consider a graph G built from the triangulation T as follows:

The vertices of G are the members of T plus the area outside the triangle. Two vertices are connected with an edge if their corresponding areas share a common border with one endpoint colored 1 and the other colored 2.

Note that on the interval AB there is an odd number of borders colored 1-2 (simply because A is colored 1, B is colored 2; and as we move along AB, there must be an odd number of color changes in order to get different colors at the beginning and at the end). Therefore the vertex of G corresponding to the outer area has an odd degree. But it is known (the handshaking lemma) that in a finite graph there is an even number of vertices with odd degree. Therefore the remaining graph, excluding the outer area, has an odd number of vertices with odd degree corresponding to members of T.

It can be easily seen that the only possible degree of a triangle from T is 0, 1 or 2, and that the degree 1 corresponds to a triangle colored with the three colors 1, 2 and 3.

Thus we have obtained a slightly stronger conclusion, which says that in a triangulation T there is an odd number (and at least one) of full-colored triangles.

A multidimensional case can be proved by induction on the dimension of a simplex. We apply the same reasoning, as in the 2-dimensional case, to conclude that in a n-dimensional triangulation there is an odd number of full-colored simplices.

Generalizations

Sperner's lemma has been generalized to colorings of polytopes with n vertices.. In that case, there are at least n-k fully labeled simplices, where k is the dimension of the polytope and "fully labeled" indicates that every label on the simplex has a different color. For example, if a polygon with n vertices is triangulated and colored according to the Sperner criterion, then there are at least n-2 fully labeled triangles. The general statement was conjectured by Atanassov in 1996, who proved it for the case k=2.[1] The proof of the general case was first given by de Loera, Peterson, and Su in 2002.[2]

Applications

Sperner colorings have been used for effective computation of fixed points. A Sperner coloring can be constructed such that fully labeled simplices correspond to fixed points of a given function. By making a triangulation smaller and smaller, one can show that the limit of the fully labeled simplices is exactly the fixed point. Hence, the technique provides a way to approximate fixed points.

For this reason, Sperner's lemma can also be used in root-finding algorithms and fair division algorithms.

E. Sperner has presented the development, influence and applications of his combinatorial lemma in [3].

See also

References

  1. ^ K. T. Atanassov (1996). "On Sperner's Lemma". Stud. Sci. Math. Hungarica 32: 71–74. 
  2. ^ Jesus de Loera, Elisha Peterson, and Francis Su (2002). "A polytopal generalization of Sperner's Lemma". Journal of Combinatorial Theory Series A 100 (1): 1–26. doi:10.1006/jcta.2002.3274. 

3.^ E. Sperner, Fifty years of further development of a combinatorial lemma,

               Part A, p.183-197,
               Part B, p.199-214,
               in: Numerical solutions of highly nonlinear problems, 
                   Fixed Point Algorithms and Complementarity Problems,
                   W. Forster (Ed.), North-Holland, Amsterdam, 1980.

External links